Las chicas solo quieren sumar

Para despedir el curso... ¿seréis capaces de resolver el problema del muñeco de nieve? ¡Felices vacaciones!

Las chicas solo quieren sumar from Eva M Perdiguero on Vimeo.

Secuencia didáctica

 UNIDAD DIDÁCTICA PARA 2º ESO:

LOS CUERPOS GEOMÉTRICOS

 

Fase I: Presentación

- La fórmula de Euler: Os hemos repartido a cada uno de vosotros un cuerpo geométrico y una ficha. Por turnos, os iré haciendo una serie de preguntas. En primer lugar, os pediré que identifiquéis, utilizando la ficha, el cuerpo geométrico que os ha tocado. Presta atención, porque hay figuras repetidas, y a lo mejor tienes la misma que un compañero o compañera. A continuación, cuenta el número de caras (c), vértices (v) y aristas (a). Toda la clase, anotaremos el resultado de dicho recuento en una tabla. Aplica la siguiente fórmula: c+v-a. ¿Qué resultado obtienes? ¿Qué resultado obtenemos con los demás cuerpos? ¿Sabes a quién se debe dicho descubrimiento? ¿Podríamos hacerlo con un cilindro? ¿Y con un cono?

- Lectura: El cíclope matemático, dedicado al matemático Euler. En la ilustración, Euler escribe en la pizarra la siguiente fórmula "c+v=a+2". ¿Coincide con la que habíamos descubierto en clase?

- Vamos a ver fotos de varios edificios de distintas épocas y lugares. ¿Qué cuerpos geométricos encuentras en ellos? ¿Cuáles son poliedros? ¿Cuáles son cuerpos de revolución? ¿Cuáles están formados por la composición de varios cuerpos distintos?

Fase II: Comprensión

 

- Trabajo colaborativo: grupos de expertos o "puzzle". En este enlace, Pere Pujolás describe la técnica. Organizamos la clase en equipos para aprender los conceptos más importantes del tema. En cada equipo, tendremos un experto o experta en prismas, otro en pirámides, otro en poliedros regulares y otro en cuerpos de revolución. Los grupos de expertos tendrán que descubrir las características del cuerpo que les ha tocado (elementos, desarrollo plano, fórmulas...) y transmitírsela lo mejor posible a sus compañeros y compañeras de equipo. ¡Ojo!, al terminar la actividad haremos un control individual... no te despistes, puesto que ¡tu equipo te necesita para hacerlo bien!

- Experiencia con sólidos transparentes.
Cada uno de los cuatro equipos va a recibir dos cuerpos geométricos: un prisma y una pirámide, o bien un cilindro y un cono. Observadlos bien, porque la pareja de poliedros o cuerpos de revolución que acabáis de recibir tienen varios elementos comunes, pero también algunas diferencias. ¿Son iguales de altos? ¿Cómo son sus bases?  Pero si los llenáramos de agua, ¿en cuál de los dos cabe más cantidad?
Nos iremos a la fuente, y allí trataremos de ver cuántas veces llenamos de agua el cuerpo de menor capacidad para rellenar el de mayor capacidad. Nos llevaremos también una probeta para medir y comparar sus capacidades.

Y ya en la clase, los distintos equipos expondrán sus resultados.

Escribe en tu cuaderno tus conclusiones.

Vamos a buscar la fórmula del volumen de los cuerpos geométricos con los que acabamos de trabajar. ¿Encuentras alguna relación entre dichas fórmulas y los resultados de los experimentos?

- Construimos un dm3 y un cm3. Con cartulina, construimos un dado de un dm de lado y otro de un cm de lado. ¿Cuántos cm3 necesitamos para conseguir un dm3?

Aprende en el libro las medidas de volumen.

¿Sabías que en el dado de un dm de lado cabe un litro? ¿Y que en el dado pequeño cabe un ml?

Fase III: Práctica

- Ejercicios para calcular volúmenes.
- Ejercicios para practicar con las medidas de volumen y capacidad.
- Hay también montones de ejercicios en el libro.

Fase IV: Evaluación

- Calcular la capacidad de un envase:
Para la clase del lunes, traemos de casa envases (latas de guisantes, de refresco, tetrabriks de distintos tamaños, cajas, etc.). Vamos a calcular su capacidad. Para ello:

1. Toma las medidas del envase. ¿Qué necesitas medir?
2. Utiliza la fórmula adecuada para calcular su volumen. Puedes utilizar la calculadora.
3. ¿En qué unidad estás expresando el volumen? Traduce tus resultados a ml.
4. Ahora mide su capacidad con una probeta. También puedes consultar la etiqueta del producto.
5. Compara tus cálculos con la medida real de la capacidad. ¿A qué se debe la diferencia en ambas medidas? ¿Te parece un buena aproximación?

Elabora en tu cuaderno un informe en el que describas las distintas actividades que has realizado, así como los resultados obtenidos. Esta actividad la evaluaremos con una nota de clase.

Fase V: Transferencia

- ¿Por qué las latas de refresco son "redondas"? 
 ¿Te imaginas una lata con forma de prisma? Debe haber alguna razón para que todas las fábricas hagan las latas iguales.
¿De qué material están hechas? ¿Es fácil y barato de obtener?

Vamos a calcular cuánto alumnio necesitamos para fabricar una lata normal, y cuánto necesitamos para fabricar una lata estrafalaria con forma de prisma, de cono... ¿Cuál es el envase más barato?

Reciclar alumnio es un 95% más barato que extraerlo de la naturaleza.

Puedes buscar en internet información sobre el reciclaje del aluminio.  

Y por último, vamos a elaborar con Glogster un cartel para explicar todo lo que hemos aprendido sobre las latas de refresco.

Por cierto, las latas no son "redondas"... ¡Son cilíndricas!

Thales midió la altura de la Gran Pirámide

Geómetra griego y uno de los siete sabios de Grecia. Fue el primer matemático griego que inició el desarrollo racional de la geometría.Tuvo que soportar durante años las burlas de quienes pensaban que sus muchas horas de trabajo e investigación eran inútiles. Pero un día decidió sacar rendimiento a sus conocimientos. Sus observaciones meteorológicas, por ejemplo, le sirvieron para saber antes que nadie que la siguiente cosecha de aceitunas sería magnífica. Compró todas las prensas de aceitunas que había en Mileto. La cosecha fue, efectivamente, buenísima, y todos los demás agricultores tuvieron que pagarle, por usar las prensas.

Hacia el año 600 antes de Cristo, cuando las pirámides habían cumplido ya su segundo milenio, el sabio griego Thales de Mileto visitó Egipto.

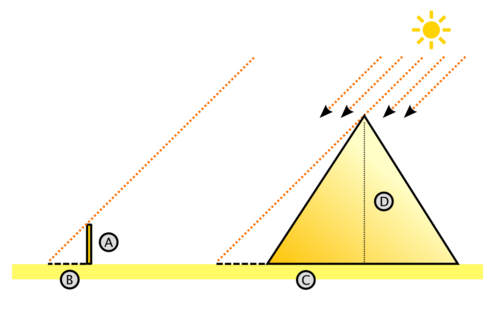
El faraón, que conocía la fama de Thales, le pidió que resolviera un viejo problema: conocer la altura exacta de la Gran Pirámide. Thales se apoyó en su bastón, y esperó. Cuando la sombra del bastón fue igual de larga que el propio bastón, le dijo a un servidor del faraón: "Corre y mide rápidamente la sombra de la Gran Pirámide. En este momento es tan larga como la propia pirámide". 

Thales era ya famoso desde que, en el año 585 a.C., predijo con toda exactitud un eclipse de sol.

Del  blog "Historias de  matemáticos"